Generate Circulant Matrix from given Array

Given an array A[], the task is to find the circulant matrix made by this array. 

A circulant matrix is a square matrix of order N x N, where each column is composed of the same elements, but each column is rotated one element to the bottom relative to the preceding column. It is a particular kind of Toeplitz matrix. 

Here is the general form of a circulant matrix.

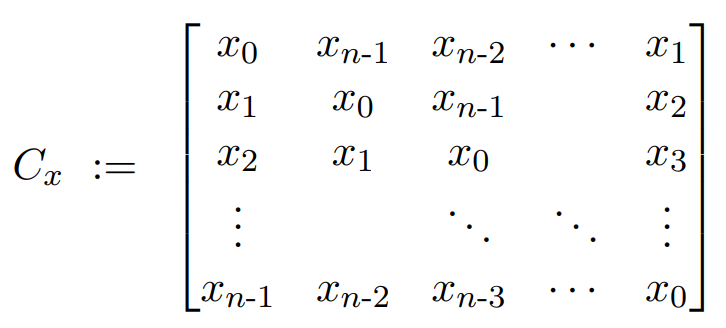
General structure of Circulant Matrix

Examples:

Input: a[] = {2, 3, 4, 5}. 
Output: Then the resultant circulant matrix should be:
2 3 4 5
3 4 5 2
4 5 2 3
5 2 3 4

Input: a[] = {0, 4, 0, 7, 9, 12, 17}. 
Output: The resultant circulant matrix should be:
0     4     0      7       9     12    17
4     0     7      9      12    17     0
0     7     9     12     17     0     4
7     9    12    17      0      4     0
9     12  17     0       4      0     7
12   17   0      4       0     7     9
17    0    4      0       7     9    12

Approach: This is a simple implementation based problem based on the following idea:

For each ith column, insert the first element of the array at ith row and insert all the other elements iterating through the column in a circular manner.

Follow the below steps to solve the problem:

  • Initialize an empty matrix (say c[][])of order N.
  • Iterate through the columns from i = 0 to N-1:
    • Iterate through the rows using a nested loop from j = 0 to N-1.
      •  if (i > 0), then assign c[j][i] = c[j – 1][i – 1].
      • else, assign c[j][i] = c[N – 1][i – 1].
  • At last, display the circulant matrix.

Below is the implementation of the above approach:

Java

  

import java.io.*;

  

class GFG {

  

    

    public static void circulant(int arr[], int n)

    {

        

        

        int c[][] = new int[n][n];

        for (int k = 0; k <= n - 1; k++)

            c[k][0] = arr[k];

  

        

        for (int i = 1; i <= n - 1; i++) {

            for (int j = 0; j <= n - 1; j++) {

                if (j - 1 >= 0)

                    c[j][i] = c[j - 1][i - 1];

                else

                    c[j][i] = c[n - 1][i - 1];

            }

        }

  

        

        for (int i = 0; i <= n - 1; i++) {

            for (int j = 0; j <= n - 1; j++) {

                System.out.print(c[i][j] + "t");

            }

            System.out.println();

        }

    }

  

    

    public static void main(String[] args)

    {

        int N = 4;

        int A[] = { 2, 3, 4, 5 };

        circulant(A, N);

    }

}
Output

2 5 4 3 3 2 5 4 4 3 2 5 5 4 3 2

Time Complexity: O(N2)
Auxiliary Space: O(1)

By Julio MarchiPosted on