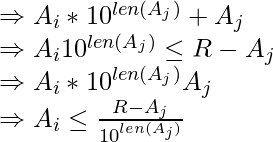Count number in given range generated by concatenating two Array elements

Improve Article

Save Article

Like Article

Given an array arr[] of size N and integers L and R defining the given range, the task is to find the number of elements in the given range that can be generated by concatenating any two elements of the array.

Examples:

Input:  N = 2, L = 10, R = 52, arr = {2, 5}
Output:  3
Explanation: All pairs available  
(2, 2) => 22 (10 ≤ 22 ≤ 52)
(2, 5) => 25 (10 ≤ 25 ≤ 52)
(5, 2) => 52 (10 ≤ 52 ≤ 52)
(5, 5) => 55 (10 ≤ 55 > 52) invalid
Hence output is 3.

Input:  N = 3, L = 100, R = 1000, arr = {28, 5, 100}
Output:  2
Explanation: The only valid pairs available  
(28, 5) => 285 (100 ≤ 285 ≤ 1000)
(5, 28) => 528 (100 ≤ 528 ≤ 1000)
Rest other pairs either fall short or higher then given range
Hence output is 2.

Approach: The idea to solve the problem is based on the following observation:

Observations:

  • The length of the valid pair is crucial as it can help us to distinguish right pairs.
  • If length is permissible we need to check whether every element is in the boundary or not.\ Rightarrow A_i * 10^{len(A_j)}+A_j leR \ Rightarrow A_i 10^{len(A_j)} leq R - A_j \ Rightarrow A_i*10 ^{len(A_j)} leR−A_j \ Rightarrow A_i leq frac{R - A_j}{10^{len(A_j)}}
  • Similarily  A_i geq frac{L - A_j}{10^{len(A_j)}}  

Follow the below steps to implement the above approach:

  • First sort the given array.
  • Find the length of the first element of the pair
  • For any pair {x, y}, x * 10len(y) + y gives the value of “xy” when they are concatenated.
  • Then, simply iterate j from 1 to N: 
    • Use the above condition to find the range where the other value (say x) will lie.
    • Use binary search to find how many possible array elements are there in the range which can assume the value x.
    • Increment the count by that much.
  • The final count is the required answer. 

Below is the implementation for the above approach:

C++

  

#include <bits/stdc++.h>

using namespace std;

  

int ValidPair(int a[], int n, int l, int r)

{

    

    sort(a, a + n);

  

    

    

    vector<int> pow10(17, 1);

    for (int i = 1; i <= 16; i++) {

        pow10[i] = pow10[i - 1] * 10;

    }

  

    int ans = 0;

    for (int j = 0; j < n; j++) {

  

        

        int len = 0;

        int cur = a[j];

        while (cur) {

            cur /= 10;

            len++;

        }

  

        

        int right = (r - a[j]) / pow10[len];

        int left = (l - a[j] + pow10[len] - 1) / pow10[len];

  

        

        

        if (left <= right)

            ans += (upper_bound(a, a + n, right)

                    - lower_bound(a, a + n, left));

    }

    return ans;

}

  

int main()

{

    int N = 2;

    int L = 10, R = 52;

    int arr[2] = { 2, 5 };

    cout << ValidPair(arr, N, L, R) << endl;

    return 0;

}

Time Complexity: O(N * logN)
Auxiliary Space: O(1)

By Julio MarchiPosted on